How To Play Kakuro

I enjoy Kakuro puzzles. They are challenging and rewarding. In this post I’ll explain:

how to play Kakuro
strategies for solving Kakuro (including Magic Blocks!)
functions used in the Excel file: VSTACK, LET, SEQUENCE (this IS an Excel blog!)

Concept

Kakuro combines elements of a crossword puzzle and a sudoku puzzle.

Rules

A Kakuro block, vertical or horizontal, has several empty squares and a square with a number (the required sum).

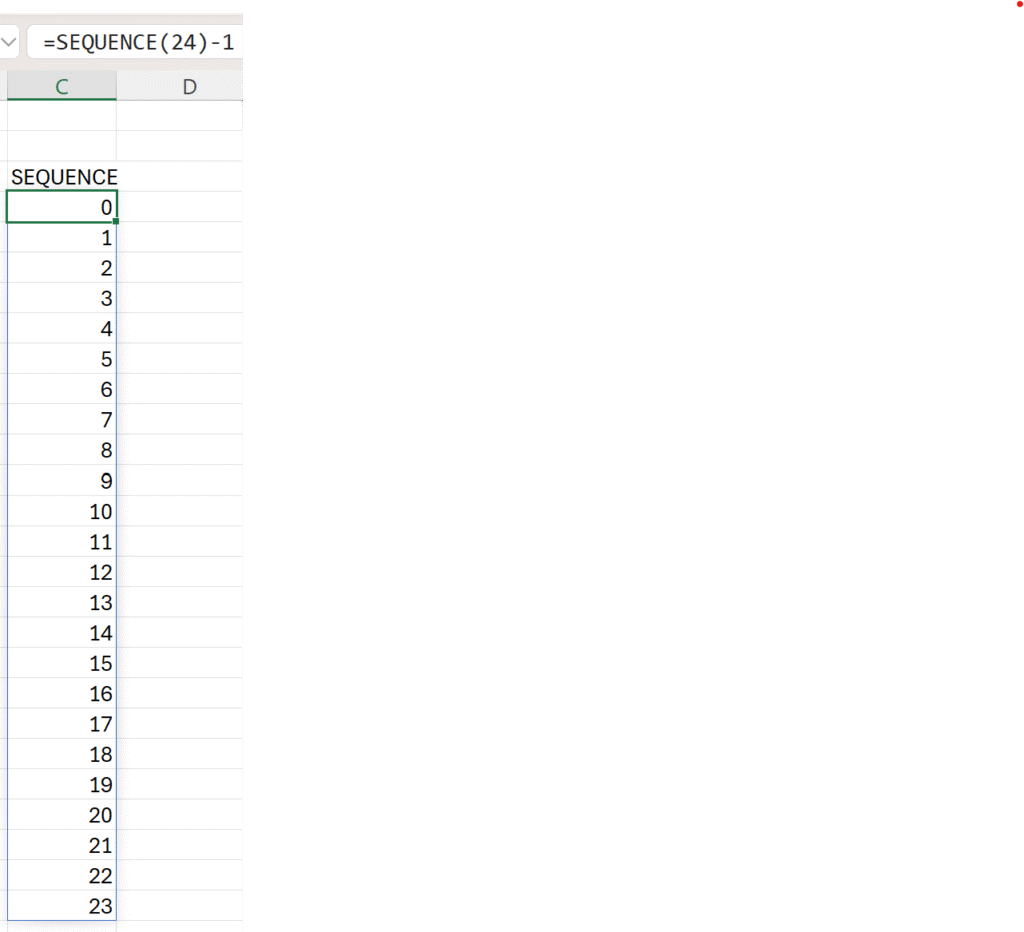
Below, a simple two block puzzle. Each block has two empty squares:

horizontal block: two empty squares that must sum to 16
vertical block: two empty squares that must sum to 17
note: these two blocks intersect and share a square

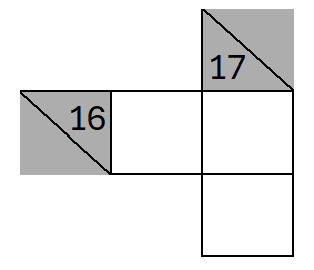
each empty square must contain a single number from 1 to 9
in a block, we can’t repeat the same number (e.g. horizontal block can’t contain 8 and 8)
when blocks intersect, the number used must work for both directions

Strategies For Solving Kakuro

Reducing combinations

Reducing the possible combinations is the key to solving Kakuro puzzles:

horizontal block: we can’t use 8 + 8 (the same number twice)
horizontal block: only 1 possible number pair: 7 + 9 or 9 + 7
vertical block: only 1 possible number pair: 8 + 9 or 9 + 8
as both blocks require a 9, let’s put the 9 in the intersecting square

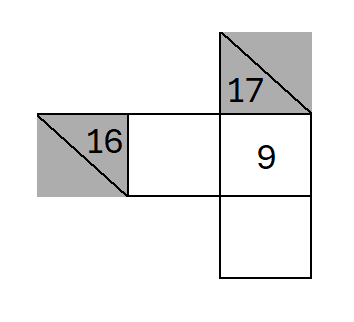
Now it’s easy! The vertical 17 needs an 8. The horizontal 16 needs a 7.

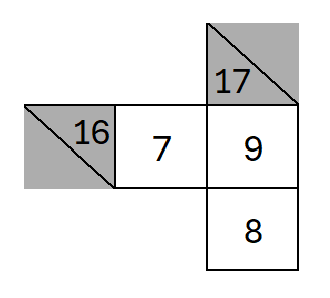
Magic Blocks

The horizontal and vertical blocks above are both magic blocks (aka unique sums). A magic block has only one set of possible numbers. The number order varies, but there’s only one set. Let’s review:

sum of 16 with 2 empty squares: 7 and 9 or 9 and 7 (no other number sets)
sum of 17 with 2 empty squares: 8 and 9 or 9 and 8 (no other number sets)

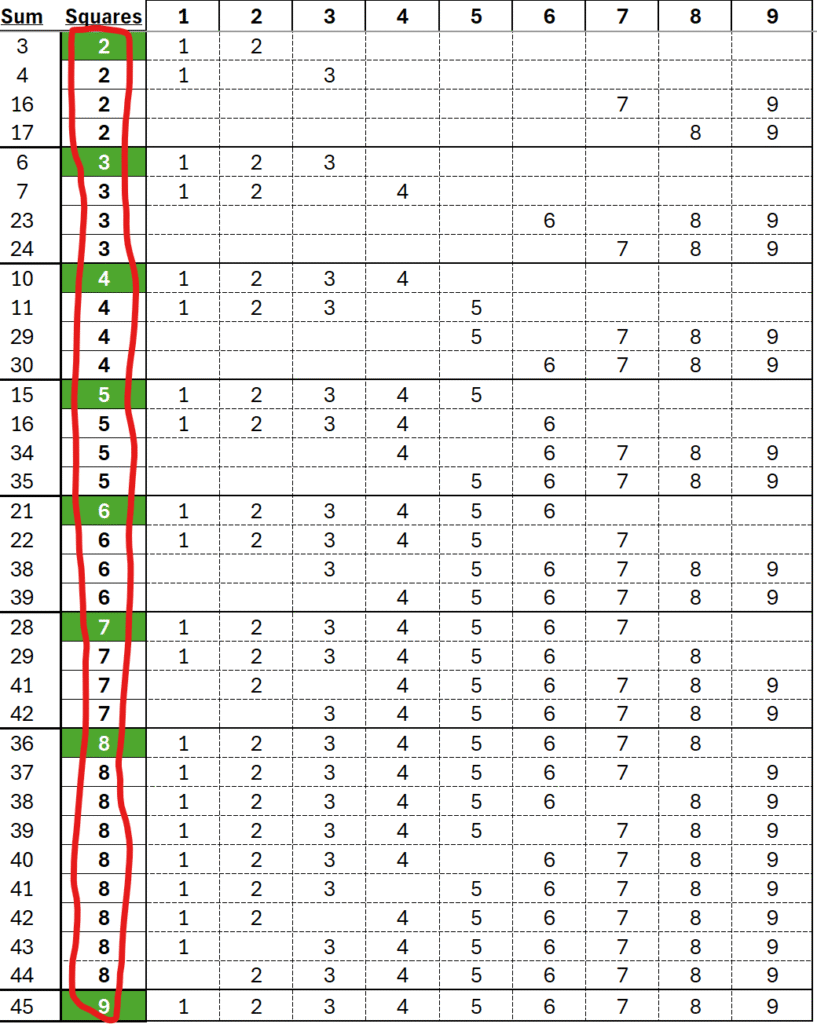
There are 34 magic blocks! Here they are:

Non Magic Blocks

There are 120 total block combinations.

34 magic blocks
86 non magic blocks

What is a non magic block? When there are two or more sets of numbers that could be added to fulfill the required sum of a block of squares. Examples:

3 squares that must sum to 8 has two options:
- 1+2+5 (any order) or
- 1+3+4 (any order)
3 squares that must sum to 10 has four options:
- 1+2+7 (any order) or
- 1+3+6 (any order) or
- 1+4+5 (any order) or
- 2+3+5 (any order)

Use sheet ‘All Combinations’ in my Excel file as a reference.

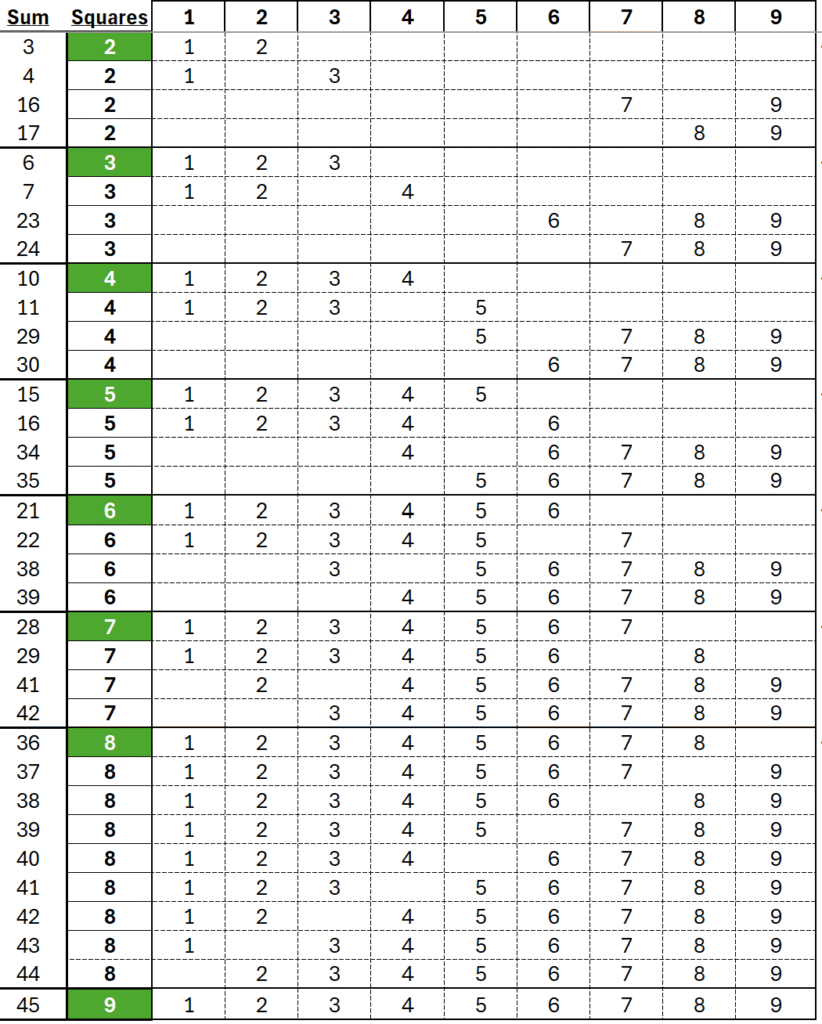
It gets complicated but when you solve a Kakuro puzzle it’s feels great! Let’s do another:

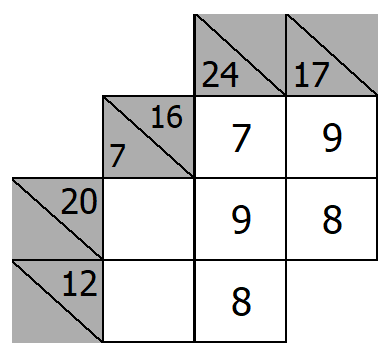
There are three vertical blocks:

sum of 7 with 2 empty squares
sum of 24 with 3 empty squares
sum of 17 with 2 empty squares

There are three horizontal blocks:

sum of 16 with 2 empty squares
sum of 20 with 3 empty squares
sum of 12 with 2 empty squares

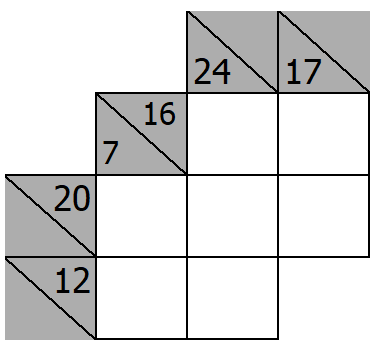
We have the same overlapping magic blocks from the previous puzzle that share a 9:

Below, we complete these two magic blocks:

A Third Magic Block: sum of 24 with three empty squares. The 8s can’t be beside each other so 7, 9, 8.

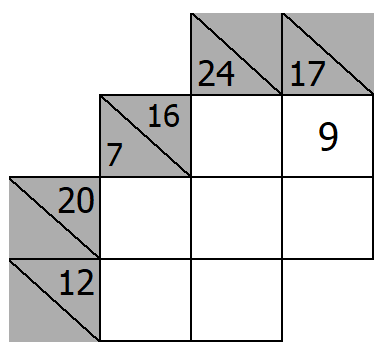
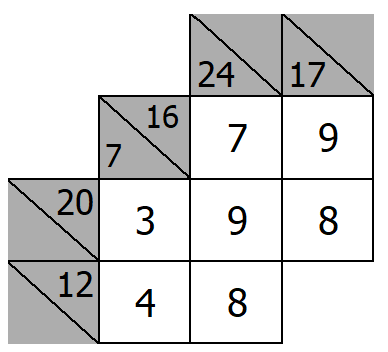
Finish the puzzle!

Sum of 20 with three squares. Two squares are already filled in. Type in 3
Sum of 12 with two squares. 8 is already there. Type in 4
Sum of 7 with two squares going down that are already filled out

when starting a Kakuro puzzle, look for magic blocks
then look for blocks with two sets of numbers (e.g. sum of 5 with 2 empty squares = 1+4 or 2+3)
use a pencil to type in possible numbers in a square. Cross them off as you eliminate numbers
double check and always use logic (never guess!)

How To Remember Magic Blocks

If your Kakuro book doesn’t list magic blocks and your internet is down, you’ll be glad you learned this method to memorize them!

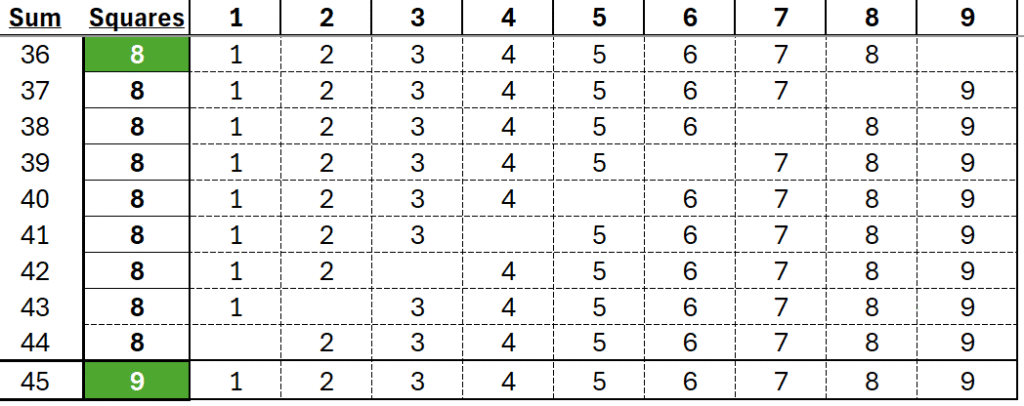
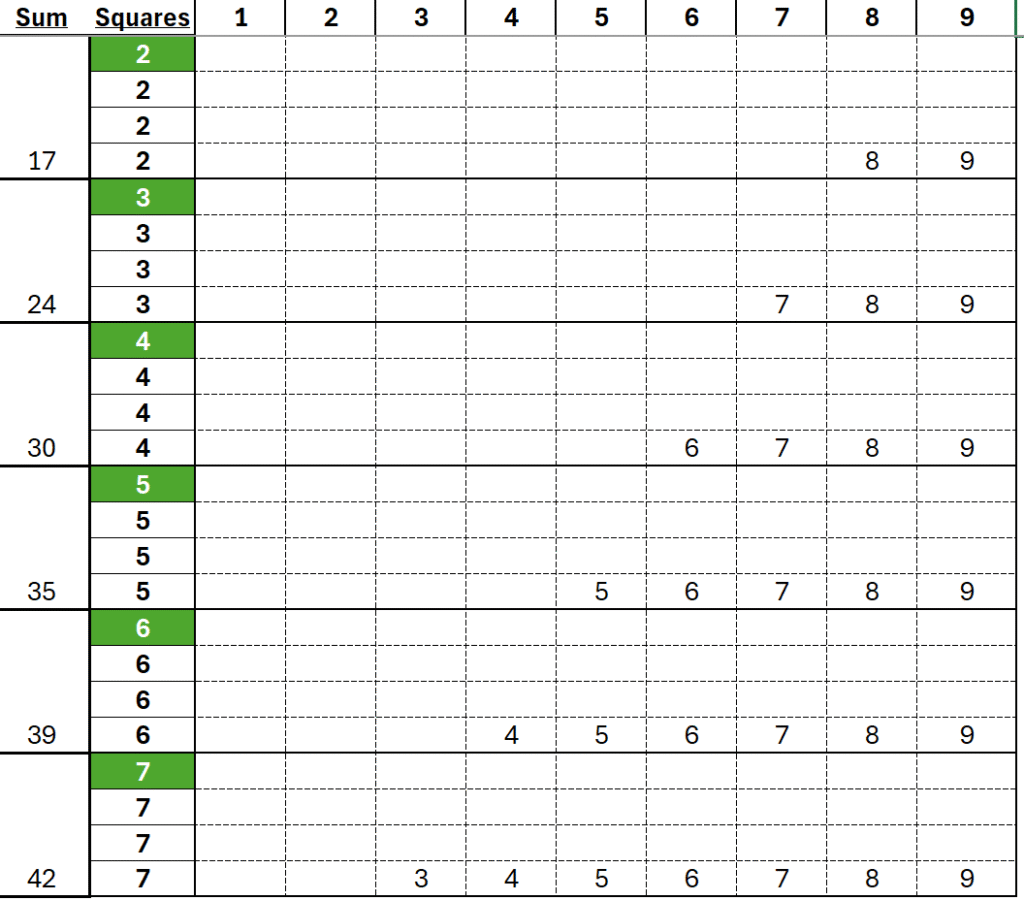
9 and 8s:

a block with 9 empty squares uses ALL 9 numbers and sums to 45
for blocks with 8 squares, it’s easy to recreate what we see below due to the empty diagonal line from top right down to the bottom left.

Below, there are four patterns used in each group of repeating squares

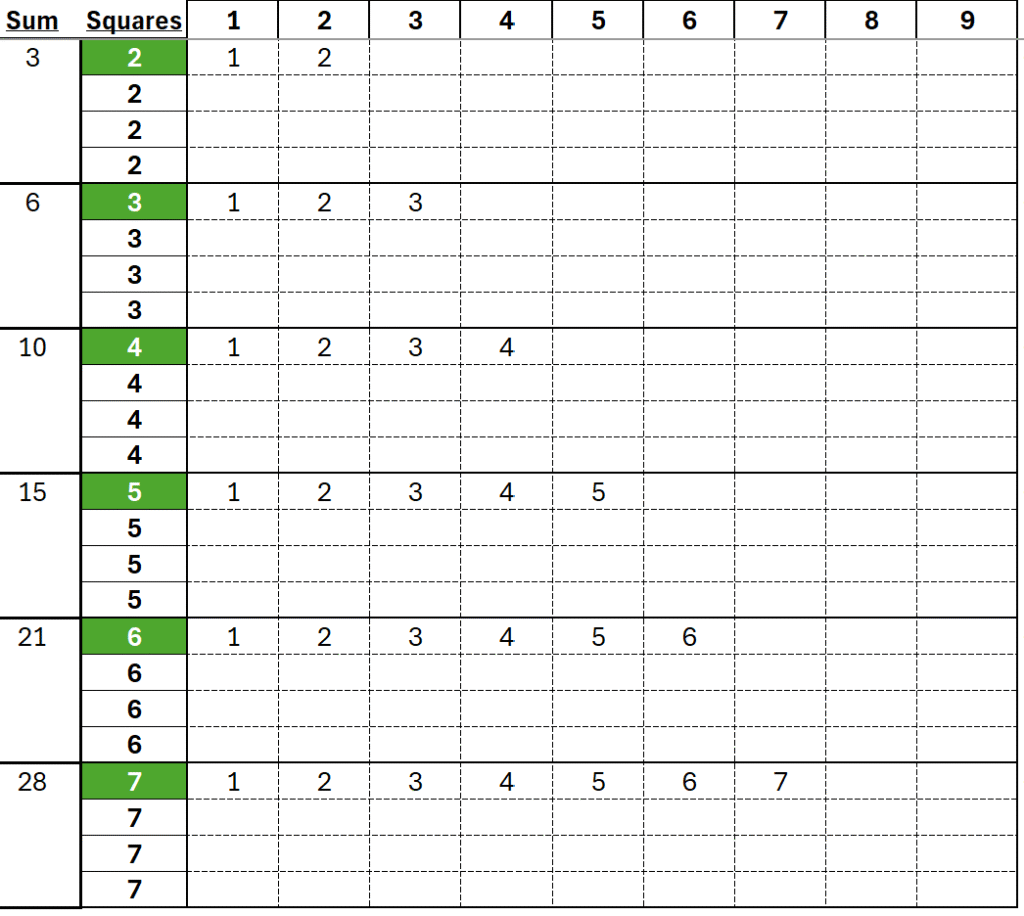
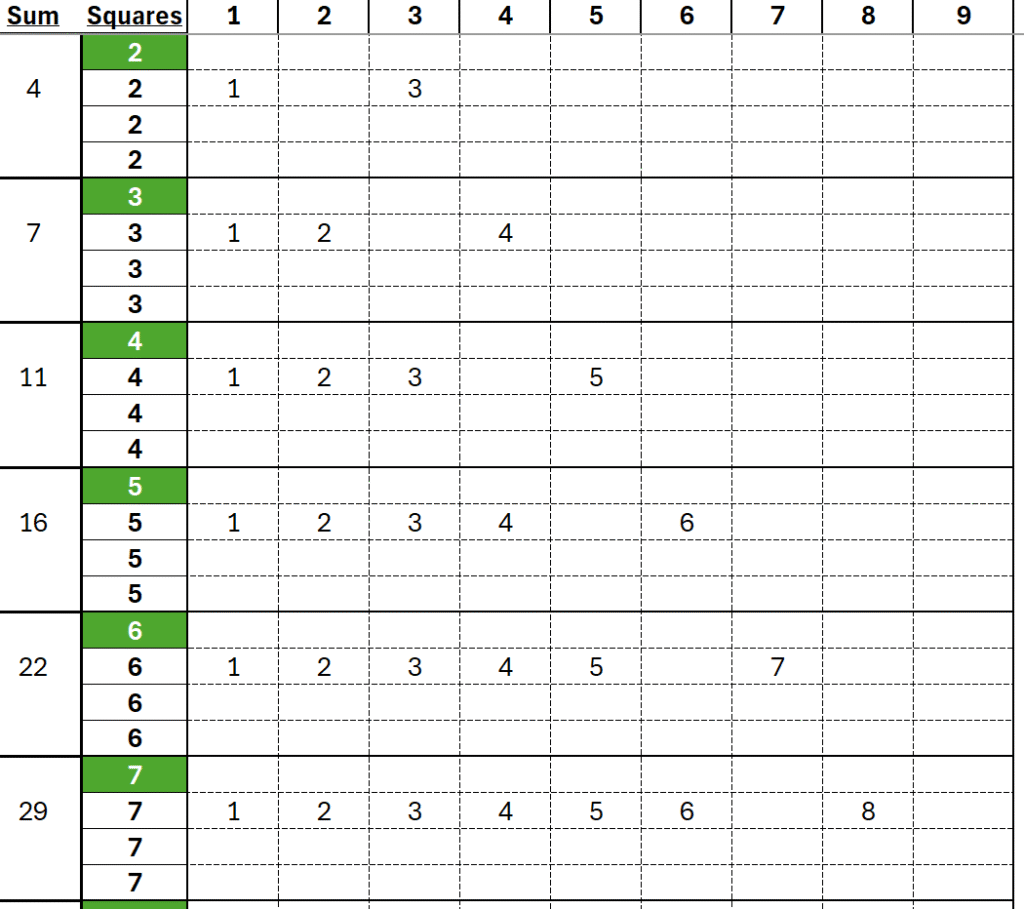
The first X numbers:

the first row in group 2 uses the first 2 numbers: 1 and 2
the first row in group 3 uses the first 3 numbers: 1, 2, and 3
…and the same for groups 4, 5, 6, and 7

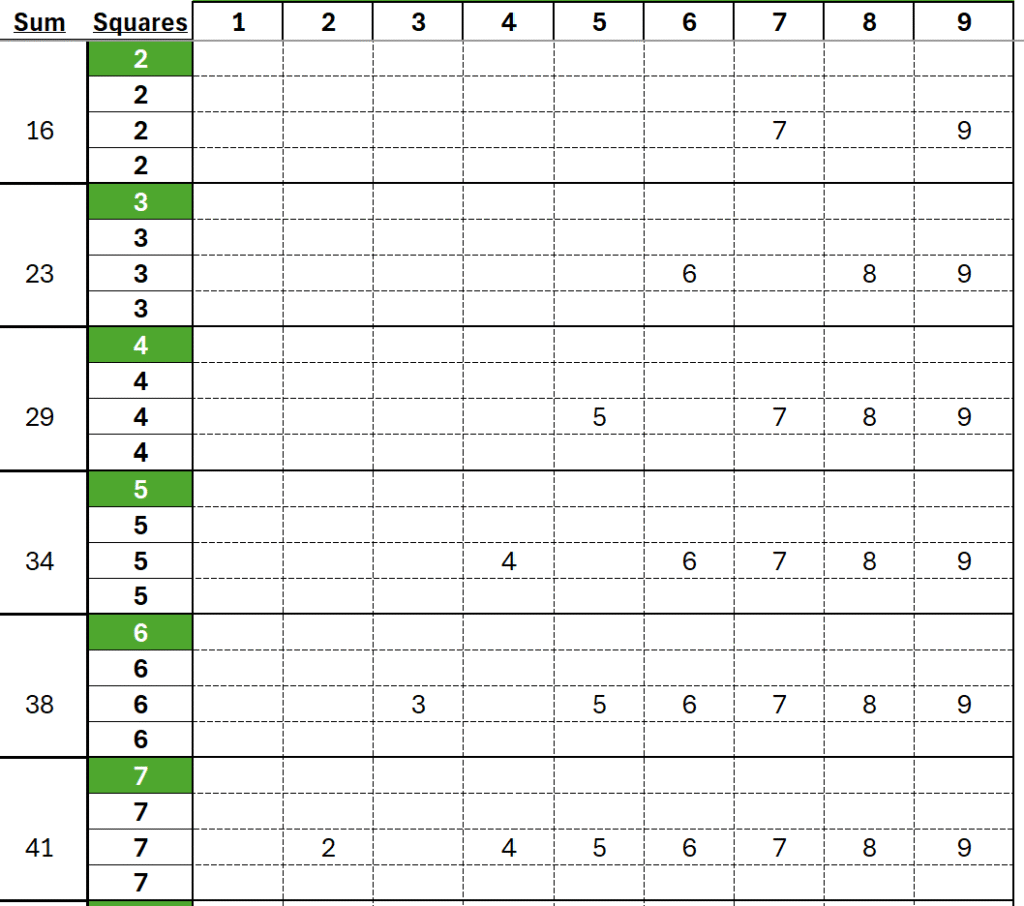
The last X numbers:

the last row in group 2 uses the last 2 numbers: 8 and 9
the last row in group 3 uses the last 3 numbers: 7, 8, and 9
…and the same for groups 4, 5, 6, and 7

The first X skip the X:

the 2nd row in group 2 uses the first 2 numbers but SKIP the 2: 1 and 3
the 2nd row in group 3 uses the first 3 numbers but SKIP the 3: 1, 2, and 4
..and the same for groups 4, 5, 6, and 7

The last X skip the X:

the 2nd last row in group 2 uses the last 2 numbers but SKIP the 2nd last
the 2nd last row in group 3 uses the last 3 numbers but SKIP the 3rd last
..and the same for groups 4, 5, 6, and 7

Functions Used in Excel File

Learn How To Play Kakuro Download

I challenged myself to write a single formula to create the numbers in the Squares column:

My idea was to first create the four repeating rows of numbers 2 to 7 and then use VSTACK to include the repeating 8s and the single 9 row.

In sheet ‘formula fun’ of the Excel file, I played around for a bit. I asked Copilot for help. It gave me this:

=LET(nums, SEQUENCE(15),
CHOOSE(QUOTIENT(nums-1,5)+1, 2, 3, 4))

This was helpful to point me in the right direction! I modified it to this:

=QUOTIENT(SEQUENCE(24)-1,4)+2

Then, I used SEQUENCE to create nine 8s and hardcoded a single 9. VSTACK vertically stacks the three parts on top of each other:

=VSTACK(
QUOTIENT(SEQUENCE(24)-1,4)+2,
SEQUENCE(9,1,8,0),
9)

Let’s examine each individual part from the inside out:

=SEQUENCE(24)-1,4)+2

This gives us the 24 rows for the four rows of numbers 2 to 7:

QUOTIENT function normally takes two numbers: a numerator and a denominator. This:

=QUOTIENT(10,4)

gives us 2 as 4 goes into 10 twice. QUOTIENT ignores the fraction (half of another 4).

But, Copilot gave the numerator multiple numbers using SEQUENCE:

=QUOTIENT(SEQUENCE(24)-1,4)+2

This is the key! Below, the result of placing the multi value sequence inside the QUOTIENT function:

The new generation of formulas that can spill results to multiple cells has really changed Excel! It’s a renaissance.

About Me

I can’t count the number of times I’ve thought “Could I make this in Excel?“

My name is Kevin Lehrbass. I’m a data analyst.

Curiosity and necessity has kept me learning for many years now. I also have to keep up with all the changes in Excel. So many new features and functions. These days I’m fascinated with Excel formulas that spill!

The site is about Microsoft Excel.

How To Play Kakuro